As reported earlier the Passing Bablok (PaBa) regression has a clear bias when the data are low precision/rounded. The calculated slopes are systematically lower.

When calculating the slope, the PaBa method involves determining the slopes of all possible pairs of data. An offset equal to the amount of slopes that have value less than -1 (b < -1) is then applied to determine the median slope.

In this study, N=10000 synthetic data sets of known slope were analyzed by first determining the offset with the 4-digit data and then redoing the procedure with the same data rounded to 2 significant digits.

Basically, the algorithm:

for 1 to N:

• generates a new data set (n=100 data) with 4 significant digits;
• calculates all possible pairwise slopes;
• determines the (b > -1) offset;
• round off the data set to 2 significant figures;
• repeats the calculation of the possible pairwise slopes;
• determines this second (b > -1) offset;
• calculates the difference between the two offsets.

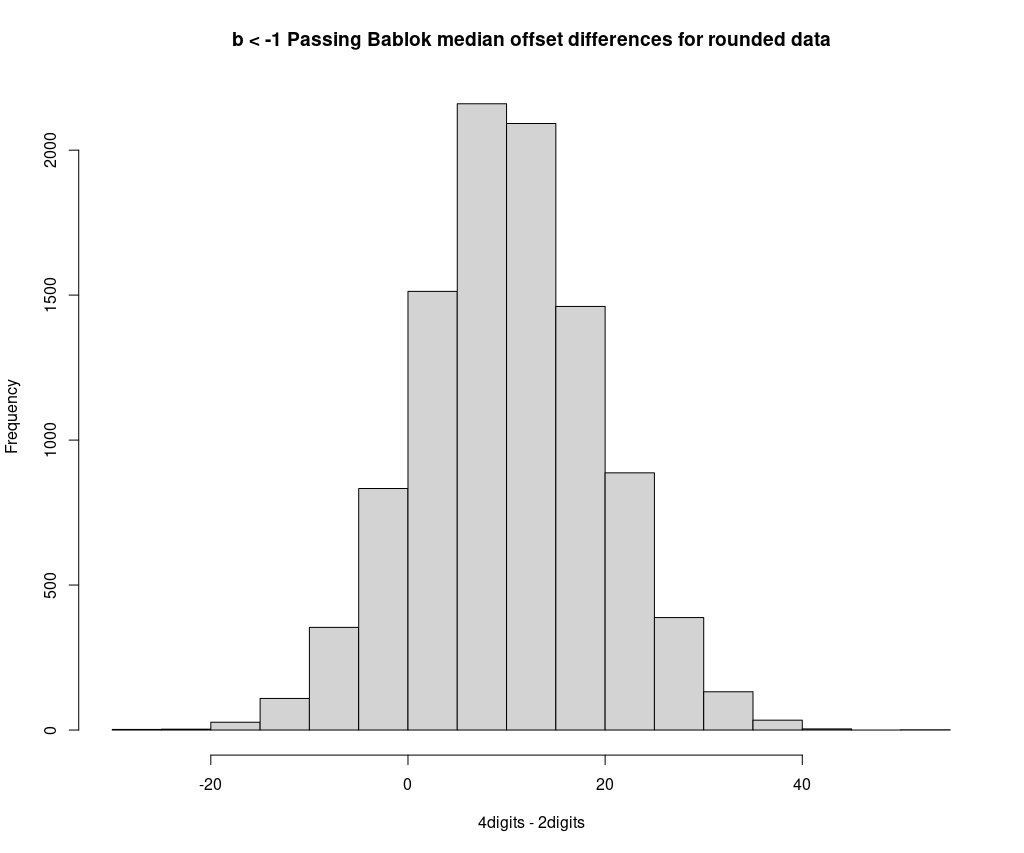
The histogram clearly shows that the differences are non-zero on average. Rounding causes a systematic reduction in the offset and thus, indirectly, also in the median slope.

This experiment suggests a potential reason for the empirical observation made with the previous simulations on regression power.

Remark

The data generating function is the same used in the 2021 paper. Scripts are available on request, of course.