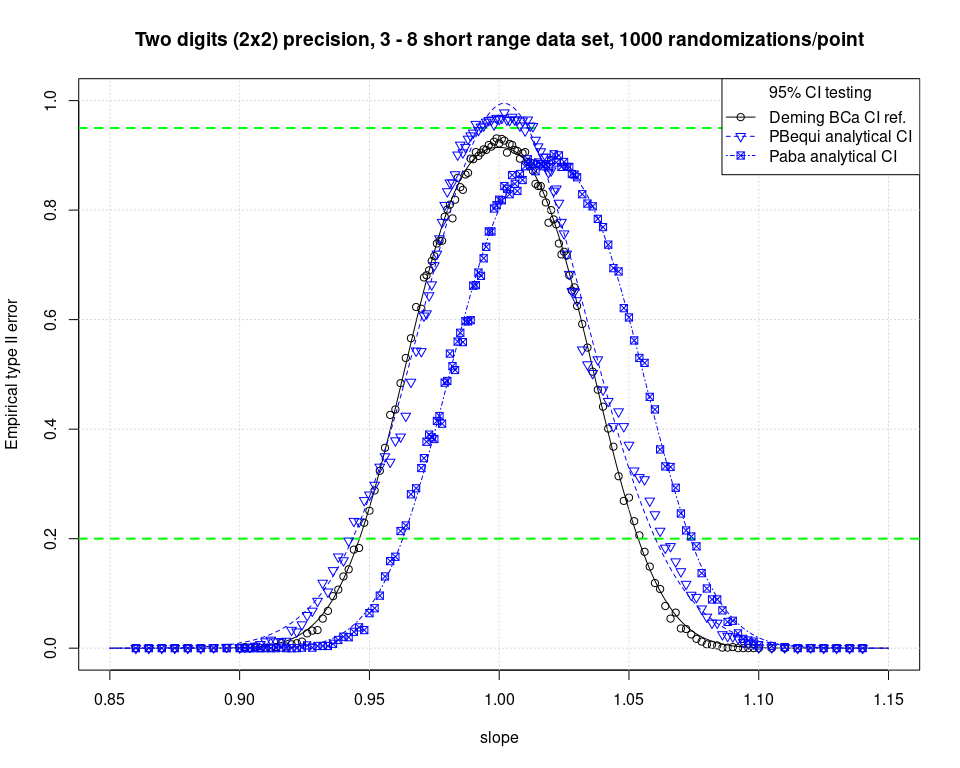
Passing Bablok (PaBa) regressions suffer from the presence of ties. A hidden source of ties is given by low precision data. In fact if the precision is low the pairwise slope calculation delivers a massive amount of slopes with the same value even if different pairs of points are used. This leads to strong erratic behaviors of the algorithms, especially for the CI determination.

It is worth noting that in the original Passing Bablok papers starting from 1983 it was clearly stated that the method was tested with 7 digits precision random generated data (32 bits actually). It was also stated that ties management could raise a lot of problems.

But for 40 years apparently nobody really took this problem as serious. Nobody tried to simulate under “real world conditions”, using rounded data with only 2 or 3 significant digits. In 2021 Pioda investigated it ad the results were stunning (Chap 2.6, pag. 31). Classic PaBa algorithm is heavily biased if the fed data has only 2 or 3 digits of precision. And all different CI methods are affected. Analytic CI are biased, bootstrapped CI are biased, too.

Recently in the new version of the R {mcr} package the “equivariant Passing Bablok” regression is available Jakob Raymaekers, F. Dufey, arxiv, 2022 with the option “method.reg=PBequi” for the function mcreg().

This version of PaBa is a step forward in that it can be used even in the case where the null hypothesis does not strictly involve an intercept of zero and a slope of one. In fact, any use of the traditional 1983 PaBa method outside these conditions is generally not correct.

Unfortunately this refurbished Passing Bablok method is less biased, but indeed still biased, as it is visible in the figure above.

This fact sounds like a “requiem for Passing Bablok”. It’s not possible to imagine laboratory managers being aware of the correct use of PaBa based on data precision. And honestly said, perhaps 60-70% of all method comparison validations are executed with data with 2 or 3 digits precision. Only few analytic methods deliver 4 digits or higher precision. A large part of the method comparisons executed in the last 40 years are simply wrong, with an higher chance to validate slopes that are higher than 1. Using a biased method to overcome the well known sphericity problem (see https://doi.org/10.1214/aos/1176350597) of the robust M-Deming (which is indeed an EIV model) makes no sense. And with bootstrap or jackknife there is no need to bother with the degree of freedom of the coefficients. Thus M-Deming (and MM-Deming too) can be revived without big concerns. They are available in the R mcrPioda package now. And for analogous reasons also the Bayesian Deming approach can be considered as coefficients d.f. agnostic approach. This latter method is also available on R with the rstanbdp package.