Classic CI testing

Very preliminary results about Bayesian Deming method Type II error are reported here. Due to computational constraints the experiment has been limited to 250 regressions per point. The CIs for Bayesian Deming are calculated with simple quantiles and not with HDI.

The well known bias found in Passing Bablok methods caused by low precision data set is not found in Bayesian Deming regressions.

The power curve of the frequentist Deming with bootstrap / BCa CI is almost indistinguishable from its Bayesian non robust counterpart. The Bayesian Deming regression run with df=5 is also indistinguishable. The Bayesian regression run at df=1 shows a lower acceptance at slope = 1, as expected from previous experiments about Type I error. The df=2 model shows also some lower ratio at slope = 1 but the difference with df=5 is minimal.

Finally, the bias for the equivariant PaBa method is once again confirmed (green data in the plot).

Further investigations are needed to compare quantiles CIs to HDI CIs

Mahalanobis distance (MD) testing

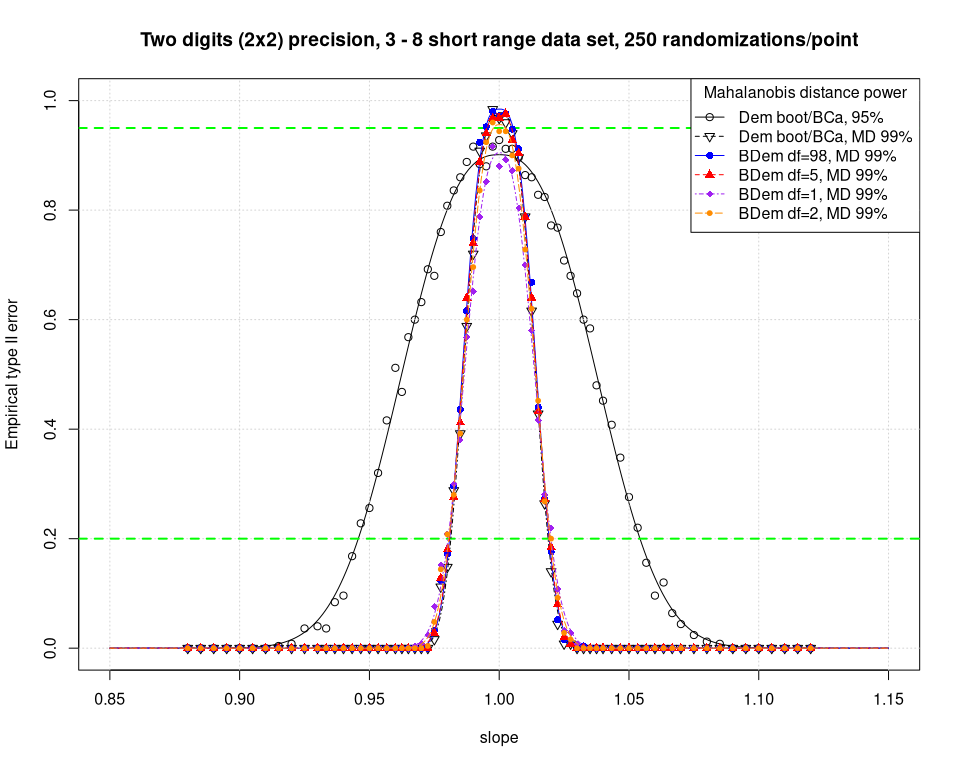
Using the Mahalanobis distance testing the power gain is strong as expected.

The Bayesian regression MD power curves are barely distinguishable from the frequentist Deming one obtained with a bootstrap procedure. Only the df=1 robust regression seems to divert slightly, showing a lower acceptance ratio at slope = 1. This observation, again, confirms the results on the Type I error investigation that have been recently published in this blog.

AUC integrals ratios and right side excess data will follow soon.